Lithoprobe Research Proposal 1997
Introduction
During 1997 I was funded by
Lithoprobe for research on two related PanLithoprobe proposals:
- Geodynamics of Plate Collisional Processes: A Synthesis of Lithoprobe
and Numerical Model Results (Beaumont, Quinlan and Jamieson).
- Development of Geodynamical Models for the Interpretation of Lithoprobe
Data (Beaumont)
This proposal requests funds for the continuation of project B.
Progress Report A
PROGRESS REPORT A: GEODYNAMICS OF PLATE COLLISIONAL PROCESSES: A SYNTHESIS
OF LITHOPROBE AND NUMERICAL MODEL RESULTS (Beaumont, Quinlan and Jamieson,
Lithoprobe Supporting Geoscience, 1995-1997)
Most of the Earth's continental crust consists of deformed metamorphic rocks
that formed deep within mountain belts. Lithoprobe has produced seismic images
of the continental crust within mountain belts ranging in age from over 3
billion years old to the present day. Understanding how, where, and when
deformation and metamorphism takes place contributes substantially to how these
seismic images are interpreted, as well as to a general understanding of how
continents and mountain belts have evolved throughout geologic time.
The Dalhousie Geodynamics Group, in collaboration with other members of the
Canadian Institute for Advanced Research - Earth System Evolution Program, has
developed numerical modelling techniques that provide computer simulations of
the mechanical and thermal behaviour of the Earth's crust during plate
collisions. These `mantle-subduction' models of orogenesis are based on the
proposition that the mechanics of small orogens are controlled by sub-orogenic
subduction and surface erosion (Willett et al. 1993, Geology 21, 371-74;
Beaumont et al. 1994, Tectonophys. 232, 114-32). The model results
demonstrate styles of crustal-scale deformation that have proven useful in
interpreting data from a number of Lithoprobe transects and other orogens (eg.,
Beaumont & Quinlan 1994, Geophys. J. Int. 116, 754-83; Ellis et al.,
1996, ECSOOT transect meeting report; Schmid et al. 1996, Tectonics 15,
1036-64). The model orogens are doubly vergent, with two crustal-scale thrust
zones (termed the `pro-' and `retro-' shear zones) developed above the point
(S) where sub-orogenic lithosphere is detached and subducted.
The main objectives of proposal A were to use the complete range of numerical
model results from the mantle-subduction models to develop a series of
templates for processes at convergent boundaries, and to apply these results to
various contractional orogens studied by Lithoprobe. Susan Ellis was
responsible for a significant part of this work. To date, we have achieved the
results described below.
-
Published Lithoprobe reports describing progress in model development,
creation of templates and the application of the results in Lithoprobe studies
(see list of references [to be put on website soon]).
-
Developed and published model results with Lithoprobe applications (See
list of references [to be put on website soon]).
-
Assembled the results into an overview paper for submission to C.J.E.S.,
Ellis, S., and Beaumont, C., Models of convergent boundary tectonics:
implications for the interpretation of Lithoprobe data. This paper is an
expanded version of the 1996 Lithoprobe report and presents templates for :
subduction, collision and the subduction-collision transition; styles of
accretion during subduction; oblique collision and subduction, and; tectonic
underplating during subduction zone retreat. The templates are used to
interpret Lithoprobe data from several transects focussing on small collisional
orogens. Applications include: the modern Cascadia subduction margin; eastern
margin of the Trans-Hudson orogen; the Abitibi-Opatica belt; Silurian
deformation in Newfoundland, and the Torngat and New Quebec orogens.
-
Used models to investigate the kinematic controls on mass partitioning of
accreted material at convergent margins. Figure 1 shows a range of the results
and the deformation modes that we have recognized. The importance of the
results is that some of the controls that promote tectonic underplating (eg.
Mode C), such as subduction zone retreat and/or large slab pull of the
subducting lithosphere, can now be quantified. Conversely, processes that
prevent the subduction or tectonic underplating of accreted (yellow) material
(Mode D) are subduction zone advance (ablative subduction) and a subducting
slab that is neutrally or positively buoyant. The results help explain the
tectonics of the Cascadia margin (Mode C type) and variations on the modes
shown may apply to Archean and Proterozoic accretionary processes (see also
PanLithoprobe section of Lithoprobe Phase V proposal).
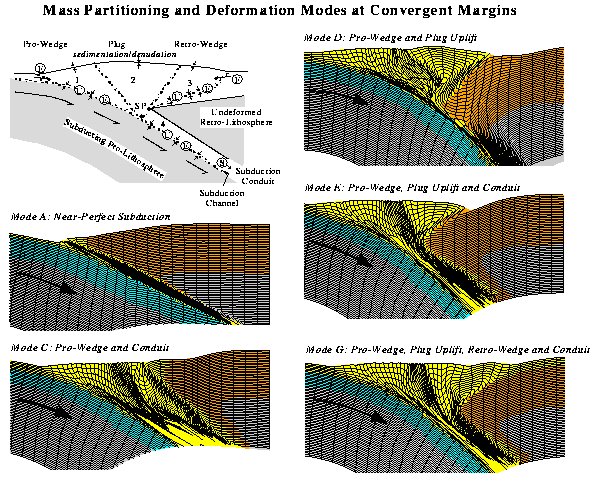
Figure 1: Modes of deformation and subduction of accreted sedimentary material
(yellow) at a convergent margin. Blue is subducting oceanic crust, orange is
continental retro-crust. Models show deformed Lagrangian grid and demonstrate
partitioning of material among pro-wedge, plug, retro-wedge and the
tectonically underplated subduction conduit. (From Beaumont, Ellis and
Pfiffner, in prep.)
Progress Report B and Proposed Research
PROGRESS REPORT B AND PROPOSED RESEARCH: DEVELOPMENT OF GEODYNAMICAL MODELS
FOR THE INTERPRETATION OF LITHOPROBE DATA
Progress and proposed research are discussed in relation to the two
parts of our 1996 proposal.
B1: IMPROVED NUMERICAL MODELS - LOCALIZATION AND THE FEASIBILITY OF 3D
COMPUTATIONS
Last year, we described progress in the development of improved numerical
techniqes needed to replace our current finite element techniques if we are to
make significant advances on both large-scale models (eg. the Lithospheric
Scale Model described in the next section) and on mesoscale structural geology
of orogens at a crustal level. Philippe Fullsack has developed a new flexible
approach to the numerical modelling - the modules of the MOZART library.
Figure 2 shows the result of a medium resolution ALE finite element
calculation of crustal scale deformation calculated using the MOZART library.
The result demonstrates some of the capabilities of MOZART, but not the full
range owing to memory (RAM) restrictions on our HP workstation (80 Mbytes) and
on the Dalhousie IBM SP-2 (128 Mbytes per cpu). The memory limit restricts
both the size of the Eulerian fe grid (801x56 nodes) and the size of the
Lagrangian grid (1334x56 nodes) used to track (advect) and regrid fields such
as material type and properties, and tensor quantities such as strain (and in
more general cases temperature, density, pressure-temperature-time evolution).
If we are granted the upgrade of the Dalhousie SP-2, computations using
Eulerian grids of 100x300 or 200x200 nodes will certainly be feasible.
However, even in the present model there is sufficient resolution (each
Eulerian element is initially less than 600x400m) to begin to investigate the
internal syles of deformation of model orogens at a crustal scale.
The figure shows the geometry and some aspects of the internal deformation of
a purely frictional model initially composed of a uniform laminate stack of
incompressible, non-cohesive dry Coulomb layers with internal angles of
friction phi=30° and phi=10°.
Deformation is driven by the uniform convergence (from left) of the base and
implied subduction at S (arrows). The model corresponds to a sandbox
experiment in which a laminate of frictionally strong and weak dry sand is
deformed by pulling a sheet along the base of the box beneath the sand on the
left (pro-) side of the box and out through a slit in the base of the box at S.
The model material does, however, differ from sand in that it does not dilate
during deformation and shows none of the strain softening or hardening
properties of deforming sand. Because the material is non-cohesive Coulomb,
the model result is independent of scale, and it may be interpreted as a
laboratory experiment, or at the crustal scale as shown.
Last year, we proposed to develop such medium resolution crustal scale models
and to investigate the dynamics of their internal modes (ie. the internal modes
of Coulomb wedges and orogenic wedges with more general properties). The model
result (Figure 2) shows that we can now compute the evolution of these models
and other experiments demonstrate that the tapers of the wedges correspond
closely with critical Coulomb wedge predictions.
|


|
|
Figure 2. ALE finite element calculation of deformation of a Coulomb
(frictional) laminate crust driven by basal velocity boundary conditions
corresponding to uniform convergence and subduction of the pro-mantle
lithosphere at S. Model has a rigid base and there is no erosion or
deposition. The model is shown for total convergence=320 km. Upper
panel shows the material
properties. White/grey layers have internal angle of friction
phi=10° and yellow layers, phi=30°. Lower panel shows
second invariant of the strain rate (red, strain rate >
10-14s-1; yellow, 10-14s-1 >
strain rate > 10-15s-1;
medium blue, 10-15s-1 > strain rate >
10-16s-1; pale blue, strain rate <
10-16s-1). The model is not `Earth like' but
demonstrates capabilities of the ALE method to make large convergence,
large deformation, medium resolution calculations. The Eulerian grid has
56 x 801 nodes and the Lagrangian grid 56 x 1334 nodes.
Note: Figure 2 in the original proposal was printed at a much larger
scale (spanning 4 pages) and also showed the Lagrangian
tracking grid superimposed on both upper and lower panels.
|
PROPOSAL. Having developed the modelling capabilities, we propose to use the
models in the two ways described below.
B1a: INVESTIGATION OF STRAIN SOFTENING / HARDENING IN MODEL OROGENS
The next logical step is to investigate the consequences of
deformation-dependent changes of material properties on the evolution of the
models. Such changes include strain-dependent hardening and softening of both
frictional (plastic) and ductile (power law viscous) rheologies in the models,
melting or other mineralogical changes, and the feedback effect of shear
heating on temperature-dependent rheological properties. The initial approach
will be to use parametric models that relate rheology to strain and/or heating
in a simple way. Although such models will not correctly represent rock
behaviour, they will allow a systematic sensitivity analysis of model response
to limited material property changes.
An important tectonic application is to determine the necessary changes in
material properties that will lead to crustal-scale changes in tectonic regime.
For example, it is generally agreed that `crustal weakening' can lead to
syn-convergent extension in orogens (orogenic collapse). However, the
relationships between crustal strength measures and gravitational/buoyancy
forces that lead to this behaviour are poorly understood. For example, is the
late-tectonic normal faulting in the orogenic core of the Southern Cordillera
caused by crustal weakening (?pegmatites), or was extension caused by a change
in boundary conditions? An equivalent problem exists for the Ontario part of
the Grenvillian orogen which exhibits extension between contractional
episodes.
B1b: INVESTIGATE THE DEVELOPMENT OF LARGER-SCALE MODEL OROGENS AND COMPARE THE
RESULTS WITH THE LARGER OROGENS STUDIED BY LITHOPROBE
When used at a crustal-scale, models of the type shown in figure 2, with more
`Earth-like' properties can be used to investigate the growth of relatively
large model orogens (sizes comparable to the Grenvillian and Cordilleran
orogens) involving several phases of subduction, accretion and collision, and
large convergence. The models also have sufficient resolution to address the
internal dynamics of the model crusts that are heterogeneous, either as a
consequence of their initial properties or their evolution. Even the model
(Figure 2) shows interesting properties that are a consequence of the potential
to create `detachments' within multiple `weak' layers. For example, the
deformation front of the retro-wedge would have a tectonic style that is like
the Grenville Front Tectonic Zone in Ontario were surface erosion efficient and
focussed on that side of the model orogen.
We propose a systematic investigation in which complexity is progressively
introduced to the models. Complexities to be considered include: layered
crustal properties (both Coulomb and thermally-activated ductility);random
heterogeneity (introduced statistically); intrusives (eg. existing large-scale
plutons and syn-tectonic intrusives and melting); surface denudation and
deposition.
B2: DEVELOPMENT OF A LITHOSPHERIC-SCALE COUPLED THERMAL-MECHANICAL MODEL
A continuing concern in regard to our current mechanical and coupled
thermal-mechanical models is that they are primarlily crust-scale models which
are forced by assumed basal boundary conditions (eg. Willett et al., 1993,
Geology, 21, p. 371-374). For example, most of our models have focussed
on the crustal response to the assumed asymmetric subduction of the mantle
lithosphere. Although we have been able to investigate the sensitivity of the
model behaviour to various combinations of the velocity of the pro- and
retro-lithospheres and the consequences of subduction zone retreat (motion of
the subduction point (S point, Figure 2) eg. Waschbusch and Beaumont (J.
Geophys. Res., 101, 28133, 1996)), the models cannot determine the
circumstances for which these boundary conditions are mechanically
consistent.
Last year, we outlined steps in the development of a lithospheric scale model
(LSM), designed to provide a better physical model for subduction/collision
processes in both oceanic and continental zones of convergence. This is
primarily a problem of density-driven flows and requires coupled solution of
the continuity, momentum and energy equations. A complete LSM model must
include lithospheric deformation and density-driven subduction in a
self-consistent manner. We proposed a series of incremental steps in the model
development.
Expand the modelled region to include the lithosphere and upper mantle so
that the entire lithosphere can be treated dynamically, not only the crust.
Investigate two types of models. Type 1, in which the velocity and slab
dip of the subducting pro-lithosphere are specified kinematically. Type 2, in
which the full density field of the modelled region is specified and subduction
is controlled by the effective slab-pull force, resistance of the viscous
mantle, total stress of the viscous mantle on the overlying pro- and retro-
lithospheric plates, coupling between them, and the coupling between the crust
and mantle lithosphere.
Several levels of approximation can be made. A good starting point (Level
1) is to produce a numerical equivalent of the laboratory experiments of
Shemenda (1993, J. Geophys. Res., 98, p. 16167) on the subduction of
hydrocarbon powder (elastic-plastic) model lithospheres in water. Reproducing
Shemenda's results is an important step in validating the new calculations.
Level 1 is a two-density model with linear/power law viscosities for
both lithosphere and fluid mantle, decoupling between the pro- and retro-
mantles, an entry flux of pro-lithosphere and a leakage flux of fluid mantle
from the model box. Level 2 introduces ductile/brittle rheologies and
model experiments are conducted for combinations of dimensionless numbers that
express changes in the absolute and relative strengths of the rheologies and
gravitational forces. Level 3, our primary goal, adds a
continental-type crustal layer to either or both the pro- and retro-
lithospheric plates. At Level 4, the degree of pro-mantle/retro-mantle
coupling is varied (by parameter choice or by introducing mantle
strain-softening rheology). At Level 5, thermomechanical coupling,
which is necessary for a fully dynamical model, replaces the assumed density
distribution. Problems like subduction in an actively convecting mantle and
the onset of subduction can also be posed.
Figures 3 and 4 show the results of Type 2 models. The results are
preliminary but encouraging, in that it was found that Type 1 models were not a
necessary precursor to Type 2 models and that Level 3/4 models with low
resolution are computationally feasible as demonstrated by these results.
The model shown has the following properties. The modelled region is 1200 km
(wide) by 400 km (deep) with a uniform 161x81 noded Eulerian computational grid
and a 801x401 uniform Lagrangian tracking grid. The 40 km thick crust is
incompressible non-cohesive Coulomb with an internal angle of friction,
phi=10° (Figure 4), but in Figure 3 the internal angle of friction is
phi=10° in the upper part (pink) and phi=4° in the lower part
(green). The 50 km thick mantle lithosphere is an incompressible Von Mises
plastic material with a yield stress sigmay=1x1010Pa.
A 50 km long initial slab (purple) of subducted pro-mantle lithosphere dips at
45°. A narrow weak linear viscous material (pale green),
eta=1019Pa s, dipping at 45° decouples the pro- and
retro-mantle lithospheres above the subducted slab. The viscous
mantle/asthenosphere has a uniform linear viscosity 1021Pa s (Figure
3) and 1020Pa s (Figure 4). Pro-lithosphere enters the upper right
side boundary at velocity, v=10-9ms-1 and this input mass
flux is balanced by a uniform leakage mass through the left and right
boundaries. Free slip is assumed parallel to the boundaries for the viscous
mantle. The lithospheric parts of the side boundaries have zero vertical
velocities and specified horizontal velocities. Subduction of the
pro-lithosphere is controlled by the density distribution, rho=2700kg
m-3 for the crust (pink/green), 3300 kg m-3 for
lithospheric mantle (orange/blue) and 3230 kg m-3 for the viscous
mantle (yellow). The
upper boundary is a free surface which deforms under the dynamic forces
generated by the model. Calculation of the deformation of the free surface and
the action of the complete weight distinguish the formulation of this model
from those commonly used for mantle convection.

Figure 3: Subduction model at timestep 2500, convergence = 250km. Only part
of model domain is shown. Grid is Lagrangian tracking grid shown at resolution
of every five elements. Materials are shown regridded on Eulerian
computational grid. Purple, orange, blue are mantle Lithosphere with same
properties. Purple is initial subducted slab. Pink is (upper crust,
phi=10°), green (lower crust, phi=4°).

Figure 4: Same as Figure 3 except fluid mantle viscosity is reduced by factor
of 10 and lower crust has phi=10°. Note how subducted buoyant crust
detaches and intrudes mantle - a possible start to the exhumation of UHP
(coesite bearing) rocks? Models are too strong to be `Earth-like' but
demonstrate computational capabilities.
PROPOSAL B2
The results (Figures 3 and 4) of the LSM are very preliminary and may contain
errors. The next steps are as follows.
-
Test and evaluate the present LSM. Specific comparisons with simple
problems, (eg. Stokes flows) for which analytical solutions exist, will be
made. Also, comparisons with tested numerical convection experiments driven by
density variations. Additional tests include : sensitivity to boundary
conditions (eg. mass flux leakage, free slip-vs-no slip); state of stress (slab
pull-vs-ridge push); accuracy of surface deformation; correct conservation of
mass, weight, vorticity, and; numerical noise caused by regridding of material
interfaces (particularly density interfaces) from the Lagrangian to Eulerian
computational grid.
-
When the LSM passes these tests, it will be recast in terms of the
non-dimensional parameters that govern its behaviour.
-
A sensitivity analysis will be made of model behaviour as a function of
non-dimensional parameter values. Anticipated behaviours include; subduction,
collision, slab breakoff, subduction zone retreat, subduction zone advance
(ablative subduction), mantle subduction etc. These results will allow a
qualitative assessment of the conditions when `mantle subduction' type
boundary conditions exist at the base of the crust (ie. when the kinematic
conditions used in our earlier models are valid).
-
Add thermal-mechanical coupling. That is, density will become a function of
temperature, in addition to material type. The production, diffusion and
advection of heat will be calculated dynamically coupled to the mechanical and
fluid flows. At this stage, we will have a fully coupled thermal-viscoplastic
mechanical model for upper mantle scale flows that evolve in a dynamically
consistent manner. This model is essential if we are to understand the
behaviour of mantle lithosphere when it is an active participant in orogenesis
(ie. not merely either rigid and undeforming or passively subducting, as
assumed in the earlier models). The results of such modelling are also
essential if we are to progress in an understanding of lithospheric (as opposed
to crustal) deformation from a Lithoprobe perspective and the results will aid
in the development of a Unified Model for orogenesis.




