Paper  starts with considerations of previous generations of thin sheet models. Three types of thin sheet approximations are in current use in geodynamics. The differences between these three main approaches are defined by the boundary conditions applied in each case (Fig1). Although all types are based on the assumption of low characteristic thickness/width ratio, these approaches have been developed independently and supported by very different additional assumptions.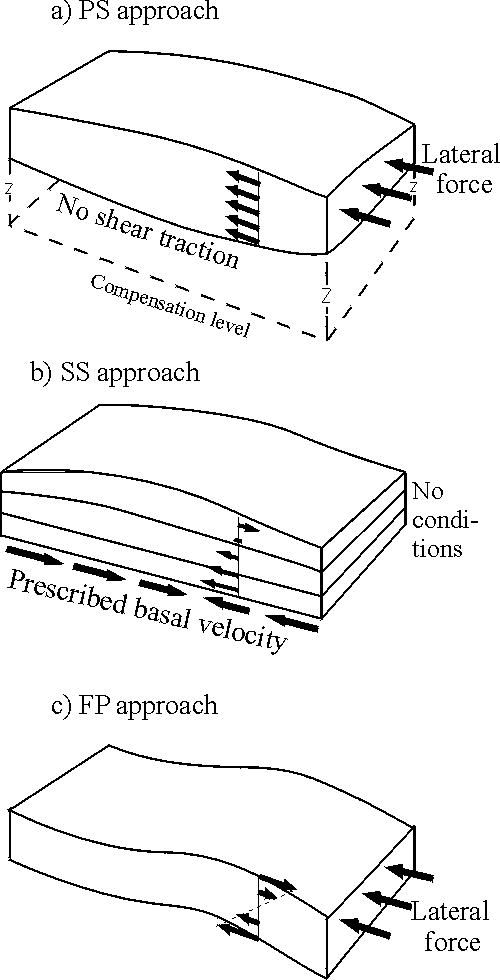 
            One (the  PS - "Pure Shear" approach) assumes a negligible vertical gradient of horizontal velocity. England and McKenzie (1982) introduced the term "thin sheet approximation" while investigating an isostatic system driven by moving the lateral boundaries with a stress-free upper surface and no shear traction along the bottom boundary (Fig. 1a). The vertical gradient of horizontal velocities can be neglected if the system is underlain by an inviscid substratum. The advantage of the PS approach is that a wide range of intercontinental collisions can be modelled by driving a stiff indentor of any shape into a thin lithosphere at any velocity  (England and Jackson 1989, Houseman and England 1993). The most significant limitations of the EM approach follow from its assumption of average rheology, its unability to satisfy a variety of horizontal boundary conditions and cannot be applied to problems involving significant layering of the lithosphere.
            The general boundary condition of the SS ("Simple Shear") approach, a prescribed basal velocity field, leads to spreading controlled by equilibration of gravity with the vertical gradient of horizontal velocity within the layer (Fig. 1b) being described by different forms of creep rheology (Zanemonetz et al. 1976, Lobkovsky and Kerchman 1991, Medvedev 1993). The advantage of the SS model is its ability to satisfy a variety of horizontal boundary conditions. The main restriction of the SS approach is that lateral boundary conditions are passive and cannot be driven.
            The FP ("Flexing Plate") approach recognises the importance of the long-term flexural rigidity of the lithosphere by ensuring equilibrium in bending moments. This approach was developed on the basis of applying thin elastic plate theory to both elastic and creep rheologies. According to this theory, a lateral force applied to a predeformed plate gives rise to moments which cause additional flexural bending (Fig. 1c). This redistributes horizontal stresses and explains geophysical observations in areas where the local compensation model (Airy isostasy) breaks down (e.g. Dubois et al. 1977, Ramberg 1970). The main advantage of the FP approach is that it can describe folding of rocks. A number of limitations generally allows only theoretical applications of this approach.
            The success of several previous attempts to combine different types of approaches has already demonstrated the great potential of thin sheet approximations (e.g. Bird 1989, Ellis et al. 1995, Aouvac and Burov 1996). However, combinations could not solve all the limitations of these approaches as is shown by analyses of the mathematics behind each of the three basic approaches. Therefore, the successful development of thin sheet approximations should be based, not on combinations of existing approaches, but on development of the fundamental analytical model behind thin sheet approximation. The expansion of asymptotic support from the low order that characterised previous approaches to a higher order results in the new extended thin sheet approximation (ETSA).
             Geodynamic 3D deformations are driven by external forces (acting on all boundaries) and controlled by rheological properties within those boundaries (Fig.2). The dynamic or kinematic boundary forces, or their combinations at both lateral and horizontal boundaries, can be specified in the ETSA. Geometric settings are required to satisfy the scaling assumption of the small thickness to width ratio that defines a thin sheet.
The model is formulated in two parts. The first part investigates mass and force balance in a thin sheet independently of its rheology. This part of the analysis was carried out in two steps: low order asymptotic approximation gives crude profiles of stresses through the thickness of the thin sheet. Those profiles were then corrected by the need for exact satisfaction of the force balance integrated over depth.  The second part employs a creep rheology to close the system of equations; a possible application of visco-elastic rheology is discussed.
            The ETSA results in a set of 2D equations expressing the integrated balance of forces in the thin sheet and rules for satisfaction of boundary conditions and reconstruction of 3D stresses and velocities. The new approach is illustrated by its application to various types of boundary conditions to present the governing systems of equations for each case.